求斜率-数学世界中的斜率：从基础到关键技能的探索

在数学的世界里，求斜率是一项基础而重要的技能。无论是在几何学、代数学还是微积分中，求斜率都扮演着不可或缺的角色。斜率不仅是一条线的倾斜程度的度量，更是我们理解曲线变化的关键。在数学的大海中，求斜率如同一座灯塔，引领我们前行。

首先，让我们回顾一下初中时学到的斜率概念。斜率代表的是直线上两点之间的变化率，也就是直线的倾斜程度。简单地说，斜率越大，直线就越陡峭；而斜率越小，直线就越平缓。在代数学中，我们通过两点间的坐标来计算斜率，这就是著名的“斜率公式”：\[m=\frac{{y_2-y_1}}{{x_2-x_1}}\]其中，\(m\)表示斜率，\((x_1,y_1)\)和\((x_2,y_2)\)分别是直线上的两个点的坐标。

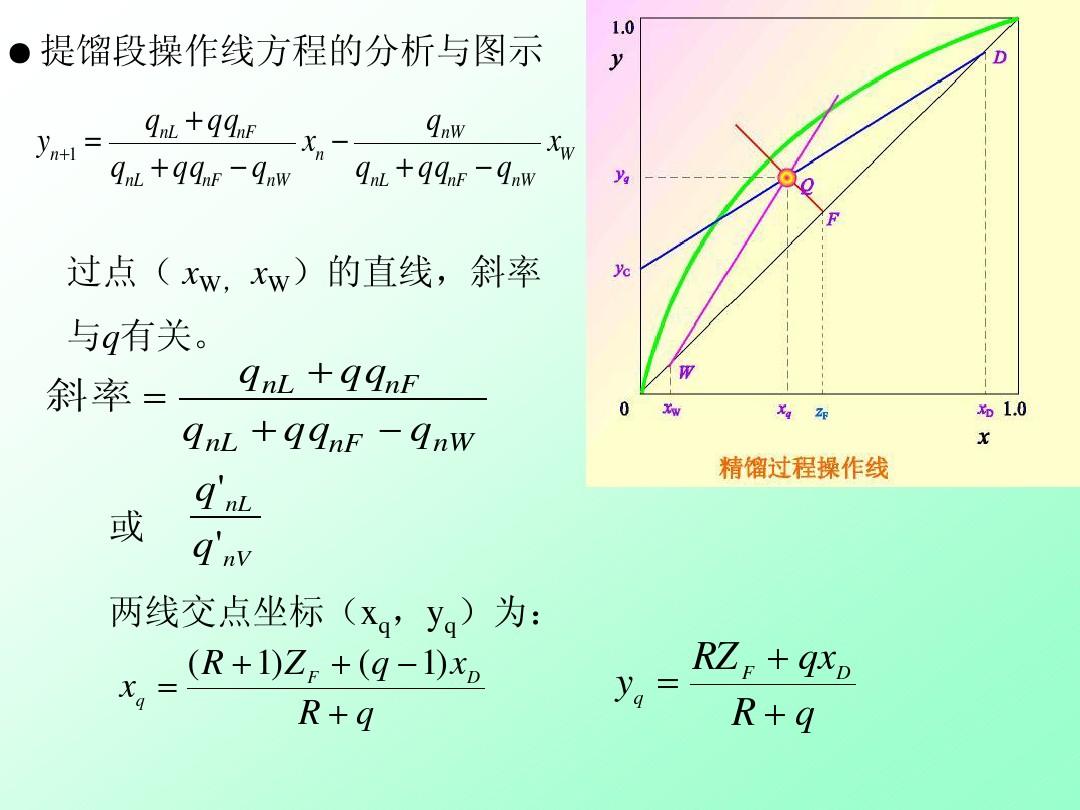
然而，斜率的应用远不止于此。在微积分中，我们学习了曲线的斜率，也就是导数。导数告诉我们曲线在某一点的瞬时变化率，这在物理学、经济学等领域都有着广泛的应用。比如，在物理学中，我们可以通过对位移关于时间的导数来得到速度；在经济学中，我们可以通过对产量关于生产因素的导数来得到边际。

tokenpocket最新版：https://sdjnez.com/yingyong/73429.html