比特币代数几何,比特币与代数几何的奇妙邂逅

比特币与代数几何的奇妙邂逅

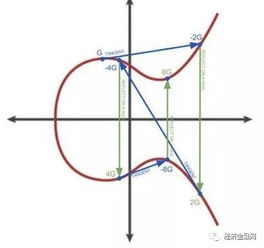
随着区块链技术的不断发展，比特币作为其最著名的应用之一，吸引了全球无数的目光。而在这背后，代数几何这一数学分支正发挥着至关重要的作用。本文将探讨比特币与代数几何之间的奇妙邂逅。

一、代数几何的起源与发展

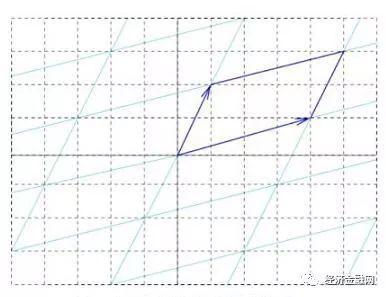
代数几何起源于17世纪，是数学的一个分支，主要研究由代数方程定义的几何图形。它将代数与几何相结合，通过研究几何图形的代数性质，以及代数结构的几何表示，为数学的发展提供了新的视角。

二、椭圆曲线在代数几何中的地位

椭圆曲线是代数几何中一类重要的曲线，它由一个二次方程定义。椭圆曲线在密码学、数论等领域有着广泛的应用。在比特币中，椭圆曲线密码学（ECC）被用来实现公钥加密、数字签名等功能。

三、比特币与椭圆曲线密码学

比特币采用椭圆曲线密码学（ECC）来实现加密和解密。ECC算法基于椭圆曲线上的离散对数问题，该问题被认为是数学上难以解决的难题。这使得ECC在加密过程中具有很高的安全性。

在比特币中，ECC算法被用于以下方面：

公钥加密：用户生成一对密钥（公钥和私钥），公钥用于接收加密信息，私钥用于解密信息。

数字签名：用户使用私钥对信息进行签名，其他人可以使用公钥验证签名的真实性。

密钥生成：基于椭圆曲线的随机数生成算法，可以生成安全的密钥对。

四、比特币地址的生成

比特币地址是用户在比特币网络中的唯一标识。其生成过程涉及到椭圆曲线密码学。以下是比特币地址生成的基本步骤：

选择一个256位的随机数作为私钥。

使用椭圆曲线加密算法，将私钥映射到一个椭圆曲线上的点。

将椭圆曲线上的点转换为比特币地址。

这个过程确保了比特币地址的唯一性和安全性。

五、代数几何在比特币领域的应用前景

更安全的加密算法：通过研究新的椭圆曲线，可以设计出更安全的加密算法，提高比特币的安全性。

智能合约：代数几何可以用于设计更复杂的智能合约，实现更丰富的功能。

量子计算：随着量子计算的发展，传统的加密算法将面临挑战。代数几何可能为量子计算时代提供新的加密方案。

比特币与代数几何的邂逅，为区块链技术的发展提供了强大的数学支持。随着研究的不断深入，代数几何将在比特币领域发挥更大的作用，为构建更加安全、高效的区块链生态系统贡献力量。