系统gmm 工具变量,GMM工具变量在系统估计中的应用解析

你有没有想过，为什么有时候我们做数据分析时，会感觉像是在解一道复杂的数学题？其实，这背后有一个强大的工具——系统广义矩估计（System Generalized Method of Moments，简称GMM）。今天，就让我带你一探究竟，看看这个工具是如何帮助我们解决那些看似棘手的问题的。

什么是GMM？

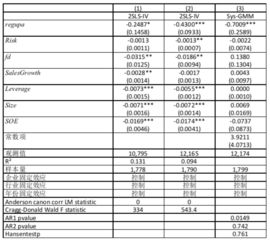
首先，得先弄明白GMM是个啥。简单来说，GMM是一种统计方法，它通过估计模型参数来分析数据。想象你面前有一堆乱七八糟的数据，你想要从中找出规律，GMM就像是一把神奇的钥匙，帮你打开这扇门。

GMM的神奇之处

你知道吗，GMM之所以神奇，是因为它能够处理那些难以直接估计的模型。比如说，工具变量（Instrumental Variables，简称IV）问题。工具变量是一种解决内生性问题的方法，它通过引入与内生变量相关但与误差项不相关的变量来估计模型参数。

工具变量：一把开启新世界的钥匙

工具变量听起来很高级，对吧？其实，它就像是一把钥匙，能帮助我们打开那些被内生性问题困扰的研究。比如说，你想研究某个政策对经济增长的影响，但这个政策可能同时影响了其他因素，导致内生性问题。这时，工具变量就能派上用场了。

GMM如何与工具变量结合？

那么，GMM是如何与工具变量结合的呢？其实，GMM通过构建一个矩条件来估计模型参数。这个矩条件是由模型中的内生变量和工具变量组成的。这样一来，我们就能利用工具变量来估计那些难以直接估计的参数了。

案例分析：房价与收入的关系

让我们用一个实际的例子来看看GMM和工具变量是如何发挥作用的。假设你想研究房价与收入之间的关系。但是，房价可能受到很多因素的影响，比如地理位置、交通便利程度等，这些都可能影响收入。这时，内生性问题就出现了。

为了解决这个问题，你可以选择一些与地理位置相关的变量作为工具变量。通过GMM，你可以估计出房价与收入之间的真实关系，而不会被内生性问题所干扰。

GMM的局限性

当然，GMM也有它的局限性。首先，选择合适的工具变量是一个挑战。如果工具变量与内生变量相关度过低，那么估计结果可能不准确。其次，GMM对数据质量要求较高，如果数据存在异常值或缺失值，那么估计结果也可能受到影响。

：GMM与工具变量的魅力

通过今天的介绍，相信你已经对GMM和工具变量有了更深入的了解。它们就像是一对神奇的伙伴，帮助我们解决那些看似复杂的问题。虽然它们有一定的局限性，但只要我们掌握好方法，就能在数据分析的道路上越走越远。

所以，下次当你面对那些棘手的数据分析问题时，不妨试试GMM和工具变量，它们可能会给你带来意想不到的惊喜哦！